[摘要] 本文是一篇建筑论文,本文基于地震学传播理论研究地震波斜入射作用下
本文是一篇建筑论文,本文基于地震学传播理论研究地震波斜入射作用下的场地反应问题,探究场地地震反应特性,对于工程选址、城市规划及重要工程设施的抗震设计提供合理的参考依据,具有十分重要的工程意义。
1 绪论
1.1 研究背景与意义
近年来地震频繁发生,造成了巨大的人员伤亡及财产损失,成为对人类威胁最严重的自然灾害之一[1]。中国处于亚欧大陆的东部,受环太平洋地震带以及欧亚地震带的严重影响,地震活动具有频度高、强度大、震源浅等特点[2]。自 20 世纪以来,全球陆地 7 级以上的强震,中国约占 35%,其中造成 20 万以上人口死亡的两次特大地震都发生在中国[3-4]。随着我国城镇化的快速推进,大量的社会资源不断地向城镇高密度聚集,致使社会经济发展深受地震灾害的严重威胁。因此,为了减轻地震带来的灾难性后果,研究地震波传播规律和场地地震反应特性问题成为现今急需解决的难题。
目前,在场地地下结构的地震反应研究之中,数值分析方法已成为主要的研究方式[5-8]。然而,在采取数值方法研究时,合理选择地震动输入方法将直接影响计算结果的精度和可靠度[9]。在工程抗震设计中,通常对地下结构的地震反应的研究大部分都是基于地震波是垂直向上传播的体波[10]。事实上,当平行的地震波在传播至地面的过程中,其到达地面时所经过的传播路径、地质条件和传播时间是不一样的,因此传播到地面的地震动必然会存在着明显的空间变化特性。这种空间变化特征主要表现为行波效应,即由地震波经传播抵达地面各处的时间差异所产生[11-13]。Jin 等[14]通过对美国西部 214 个地面地震动记录的统计分析,得出近场条件下一般基岩场地的地震波入射角变化范围在 45°至 75°之间。Takahiro 等[15]根据日本东京的 24 个近场强震记录进行反演,认为地震波在近场条件下的平均入射角为 38°,变化范围在 12.4°至 54.1°之间。因此,在近场条件下进行地下结构抗震设计时,地震波不可简单视为垂直向上入射,而应考虑以一定角度倾斜入射[16-18]。现阶段,斜入射地震波作用下的场地地震反应分析已成为地震防灾减灾工程的一个重要课题[19-20],但其研究内容相对偏少,因此本文基于地震学传播理论研究地震波斜入射作用下的场地反应问题,探究场地地震反应特性,对于工程选址、城市规划及重要工程设施的抗震设计提供合理的参考依据,具有十分重要的工程意义。
................................
1.2 研究现状
1.2.1 场地地震反应分析问题
场地地震反应分析技术可以直接为结构抗震提供相应的设计参数,是当前工程场地地震安全性评价的核心技术之一。根据 1928 年 San Francisco 大地震的震害资料,Wood 认识到场地条件对地面运动有影响以来[21],岩土抗震工程领域的学者们用定量估算的方法,对地震作用下的成层场地动力响应特征进行了广泛研究,并逐步得到了一些场地条件在工程抗震中的重要性认识。
早先出现的场地地震反应分析方法认为土体应力应变关系呈线性变化,以线弹性波动法最为显着。但是,实际的工程场地是一个三维的立体空间,假设将地震动输入看作剪切运动并将场地当作一维成层模型进行土层地震反应[22-24],则可将三维空间问题简化为一维线性问题。1968 年 Idriss 等[25]最先采用一维剪切梁模型对土层场地进行求解,分析了土层场地水平振动特性和地震反应的影响。1989 年廖振鹏等[26]提出了等效线性化方法,将复杂非线性问题简化为线性问题并将该方法应用于频域中分析。陈国兴等[27]利用分时段的设想,降低了等效线性模型产生的“虚拟共振效应”;姜通等[28]利用频率相关性思维,充分考虑高频响应,对传统等效线性化方法进行改良,使得计算结果更精确。一维空间场地反应分析的方法和相应的计算机程序至今已取得了更加全面深入的发展[29-31],但大部分的研究都是基于地震波垂直入射作用为前提,对于斜入射地震波作用下场地的非线性反应问题研究尚且考虑不足。
随着地震观测资料越来越丰富以及科学研究的深入发展,发现土体地震动响应在数值上并不是呈线性变化,因此考虑斜入射地震波作用下成层弹性半空间或者局部介质非线性响应问题更加符合工程实际[32]。李小军等[33]研究了当地震波以小角度倾斜入射时在局部非均匀介质中的场地非线性反应问题;李山有等[34-35]利用有限元法研究了地震波倾斜入射条件下台阶地形引起的波型转换和地震波倾斜入射下的断层台阶线性地震反应,说明了研究地震波倾斜入射的必要性;Heymsfield 等[32]研究了 SH 波斜入射时倾斜基岩对地表位移的影响,研究表明当入射角为 60°时地表位移幅值最大;范留明等[36-37]提出了倾斜入射地震波作用下成层场地界面子波算法和场地地震响应的快速时程算法,并通过模型计算验证了该方法的可行性。
..............................
2.1 弹性波的波动方程
在不同的介质模型中,地震波传播有不同的规律,一般介质模型越复杂,其描述地震波传播的方程就越复杂,均匀各项同性完全弹性介质是一种最简单的介质模型。本节讨论弹性波动方程的建立及其通解问题。
2.1.1 应力与应变的关系
(1)应变分析
应变分析主要讨论的是弹性体的弹性应变。一般情况下,只要得到处于应变状态下的弹性体质点位移的一般表示式,就能定量描述弹性介质应变状态。通过正应变(表示物体的压缩或拉伸)、体应变(表示体积的相对变)和切应变(表示弹性体扭转或体积元侧面角错动)的定量讨论,得到下列几何方程:

...............................
2.2 弹性分界面上的边界条件
在实际的应用当中,通常将复杂地层视为由多个分界面组成。弹性分界面也就是介质性质的不连续面,在研究地震波在弹性分界面上的传播特性时,通常认为分界面两侧的介质是紧密相连的。此时,弹性分界面上的运动将会满足位移连续和应力连续,即弹性分界面上的边界条件。下面从平面波理论出发(认为波前面是平面,它以恒定的人射角投射到分界面上),讨论平面波在单个弹性分界面上的反射和透射问题。
(1)位移连续边界

.............................
3 地层分界面上的反透射系数、能量及相位角数值解析..................233.1 P 波入射时地层分界面上的反透射系数数值解析................................... 23
3.1.1 P 波从高阻抗向低阻抗介质投射时的反透射系数............................ 24
3.1.2 P 波从低阻抗向高阻抗介质投射时的反透射系数...................... 25
4 地震作用下的地面振动反应分析.....................................44
4.1 自由表面上的边界条件.......................................44
4.2 P 波在自由表面上的反射......................................... 45
4.2.1 P 波入射时自由表面上的波形转换.......................... 45
4.2.2 P 波入射时自由表面上的反射系数.................................. 46
5 地震作用下场地反应的影响分析.........................63
5.1 地震作用下的场地反应.............................................63
5.1.1 P 波入射时场地振动反应...................... 65
5.1.2 SV 波入射时场地振动反应........................ 65
5 地震作用下场地反应的影响分析
5.1 地震作用下的场地反应
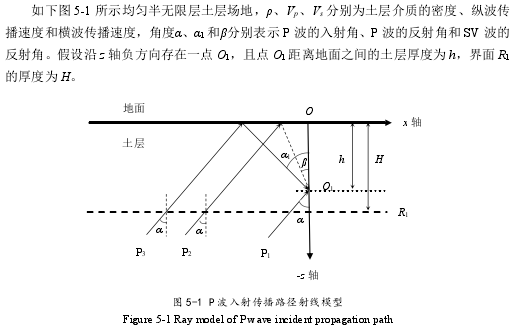
5.1.1 P 波入射时场地振动反应
...........................
6 结论与展望
6.1 结论
目前,对地震 SV 波倾斜入射的研究多局限在临界角范围之内,而对于大于临界角情况却很少涉及。即使对跨临界角相应问题有所研究,也仅仅局限于反透射系数的推导,并未对地面振动反应情况做出详细的研究。本文基于地震学原理,推导出了地震波倾斜入射作用下弹性分界面和自由表面处的反射、透射系数,进而推求了 SV 波入射发生全反射条件下的反射系数表达式,然后应用叠加原理得到弹性半空间计算方法,并编制了相应的MATLAB 计算程序,通过模型算例分别研究了地震 P 波和地震 SV 波以任意角度作用下的场地反应特性,并分析了入射角对场地地震反应的影响,得到如下几点结论:
(1)在 P 波入射情况下,随着入射角的增大,竖直振幅逐渐减小;水平振幅先增大后减小。当入射角小于 40°时,竖直振幅大于水平振幅;当入射角大于 40°时,水平振幅大于竖直振幅,且在 65°时达到最大值。
(2)在 SV 波入射情况下,场地反应随着入射角的变化与临界角的关系密切相关。当入射角小于临界角,水平振幅单调减小,竖直振幅单调增大。当入射角等于临界角时,水平振幅达到最大值,竖直振幅达到最小值。当入射角大于临界角时,水平振幅快速锐减,至 45°时减小为零,此后呈抛物线形变化,顶点位于 70°附近,其值约为 0.5,而竖直振幅单调减小。
(3)当 SV 波入射角大于临界角时,反射系数为复数,由此引起的水平振动和竖直振动也是复数,两者的相位差恰好为 0.5π,表明在简谐波作用下水平振动与竖直振动呈正交特性。
(4)地震场地反应不仅与入射角有关,还与地震波频率有一定关系,总体表现为随着频率的增大振动减弱,但不同类型的入射波对水平位移和竖直位移的影响不同。P 波入射时,当入射角小于 20°时,频率变化对水平位移影响较小,对竖直位移影响较大;当入射角度逐渐增大,频率变化对水平位移影响较大,对竖直位移影响逐渐减弱;当入射角大于 70°时,频率变化对振动位移几乎没有影响。SV 波入射时,当入射角等于临界角或是在远离临界角时,频率变化对水平位移影响较大,对竖直位移影响较小;当入射角接近临界角时,频率变化对水平位移影响较小,对竖直位移影响较大。
参考文献(略)